21st Century AI

(This blog is reposted from my other site: Dinosaur-Island.com)

A few days ago I wrote about Dinosaurs, tanks and line of sight algorithms and how my previous work in modeling and simulations (M&S) for military wargames (specifically line of light algorithms) was applicable in Dinosaur Island. Today I am working on the models for dinosaur movement, speed, and what are called “least weighted path” algorithms.

You are probably familiar with least weighted path algorithms even if the term is new to you. Least weighted path algorithms are used to calculate routes in GPS units for cars or smartphones or for various internet sites like MapQuest, Google or Bing. When calculating a route there are a number of criteria to chose from. Does the user want:

• The fastest route?
• The shortest route?
• The most fuel efficient route?
• The route that avoids certain features (such as specific terrain, topography or extreme slopes)?

These options are what ‘weight’ the potential routes in a ‘least weighted’ path algorithm. For example, taking the Interstate is often the fastest route (least amount of time) but frequently is not the shortest route (least amount of distance).

Back in grad school I did my ‘comprehensive exam’ for PhD students on the subject of least weighted path algorithms. There are two very popular algorithms that solve this problem: one is Dijkstra’s algorithm (which is an exhaustive search solution) and the other is the A* algorithm, by Peter Hart, Nils Nilsson and Bertram Raphael. The primary difference between Dijkstra’s algorithm and the A* algorithm is that Dijkstra’s is guaranteed to return the optimal solution but it often takes the most time to calculate. The A* algorithm is much faster to calculate but is not guaranteed to return the optimal (or perfect) solution. In computer games we almost always use the A* algorithm because speed of calculations (especially over large maps) is more important than having the absolutely perfect route. At the bottom of this blog are links to descriptions of these algorithms and my research paper discussing an optimization of A*.

But, what does this have to do with dinosaurs and tanks?

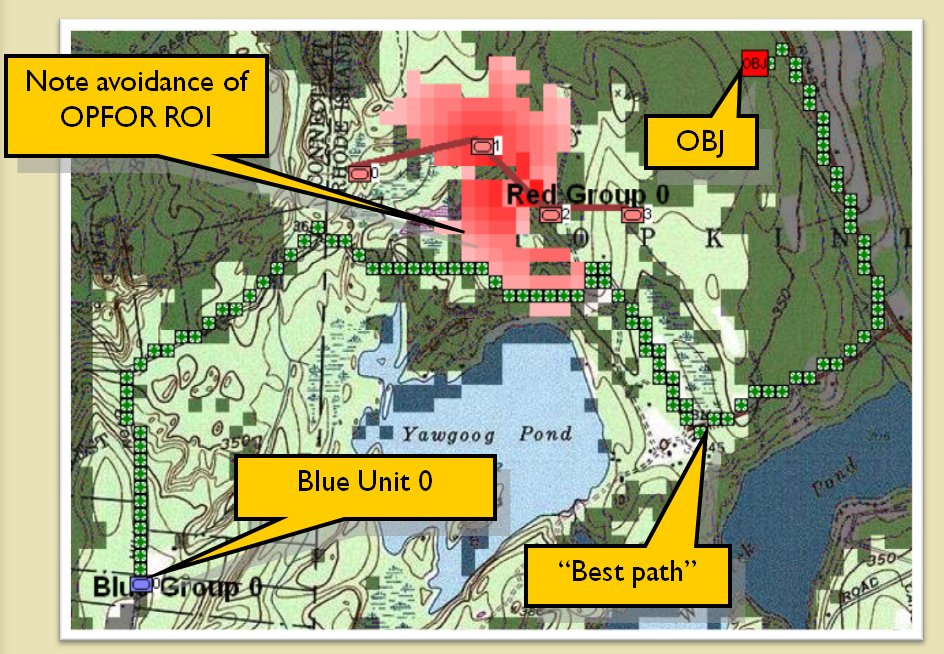
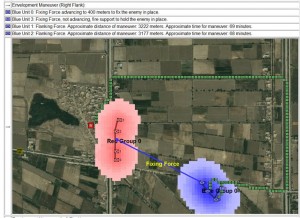
When working on an M&S involving vehicles (like tanks) our primary concern is finding the fastest way for the tank to get from Point A to Point B. Sometimes, we want the tank to avoid entering into an area where the enemy (called OPFOR, or ‘Opposition Forces’ in military parlance) can hit it with their weapons (this is called ‘range of influence’ or ROI). This is illustrated below:

We also want the tank to take advantage of roads and avoid swamps, rivers and ponds.The maximum speed of a tank traveling on a road is higher than the maximum speed of a tank traveling across a field. This is not the case with a T. rex or an Edmontosaurus regalis.

Another difference between tanks and dinosaurs is that as long as a tank has fuel it can go at 100% of their maximum speed (on a specific terrain) without problems. This simply isn’t the case with dinosaurs. As dinosaurs expend energy (and remember, energy is the ‘currency’ of Dinosaur Island, see: The currency of Dinosaur Island) they get tired and they can’t run as fast or as far. Also, dinosaurs run at their maximum speed only for short distances and only in extreme emergencies or at the very end of a hunt when they attack.

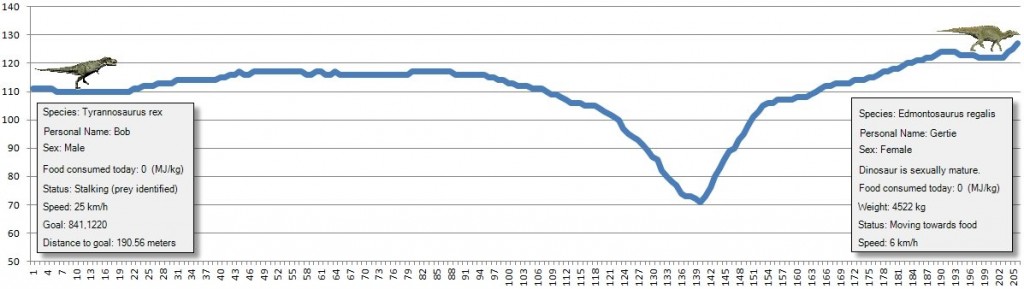
The illustration at the top of the blog also points out another major difference between tanks and dinosaurs: modern tanks (specifically the M1A1) has a published specification of being able to climb a 60 degree slope at a speed of 7.2 km/h (see here). That’s pretty impressive. It’s unlikely that that a T. rex could navigate a slope that steep. In the cross-section at the top of this blog we show the slopes that Bob, the T. rex, will encounter following a straight line to Gertie, the Edmontosaurus.

Clearly we’re going to need to use a least weighted path algorithm for calculating dinosaur movement so that they will avoid steep riverbanks and crevices. We also will create a table of ‘energy costs’ that dinosaurs will incur as they travel across various terrains (like swamp). These values will be used in our least weighted path algorithm.

Some links about least weighted path algorithms:

• Dijkstra’s algorithm on Wikipedia has a very easy to follow description with a couple of cool animations to show how it works. Link here.

• A* search algorithm on Wikipedia also has a couple of very nice animations to show how it works and pseudocode. Link here. By the way, I once sent Nils Nilsson an email asking him what the ‘A’ in A* stood for and he replied, “algorithm.” Now you know.

• “An Analysis of Dimdal’s (ex-Jonsson’s) ‘An Optimal Pathfinder for Vehicles in Real-World Terrain Maps,‘ the paper for my Comprehensive Exam can be downloaded here.